
LE FORMULE DEL TRIANGOLO RETTANGOLO
A differenza del triangolo isoscele o equilatero o ancora scaleno, il triangolo rettangolo presenta un lato interno con un'ampiezza di 90 gradi. Le formule di questo tipo di triangolo, chiamato rettangolo proprio per l'angolo retto che si forma al suo interno, sono molto semplici da studiare e mettere in pratica. Oggi le vediamo ed affrontiamo anche l'argomento teorema di Pitagora che, nei triangoli, in particolare in quello rettangolo, viene utilizzato per calcolare la lunghezza di un cateto o dell'ipotenusa.
Ma ecco la formula per calcolare il perimetro P di un triangolo :
P=b+h+l
dove b corrisponde al lato di base, h all'altezza che corrisponde al lato che forma l'angolo retto con la base b ed l al lato obliquo, detto ipotenusa del triangolo rettangolo. L'area A di un triangolo rettangolo invece è data da :
A=(bxh)/2
quindi dal prodotto della base b per l'altezza h. Ma le formule del triangolo rettangolo non finiscono qui perchè possiamo utilizzare le formule del teorema di Pitagora per trovare uno dei lati mancanti tra i 3 quando ne abbiamo 2.

Nella figura sopra potete vedere che l'ipotenusa corrisponde al lato più lungo del triangolo rettangolo e questo ovviamente sempre. L'ipotenusa è sempre il lato più lungo dei 3. La somma dei 2 cateti al quadrato e posti sotto radice ci da infatti il valore dell'ipotenusa. La formula del teorema di Pitagora è quindi :

La lettera "c" corrisponde alla lettera "i" nel disegno sopra. Di conseguenza un cateto, quindi il lato b base, si calcola con la formula inversa :
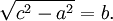
L'altro cateto del triangolo rettangolo invece :
corrispondente all'altezza h del triangolo stesso. Le formule del triangolo rettangolo finiscono qui ma quello che vi manca, per una conoscenza più approfondita, è l'enunciato del teorema di Pitagora, che recita in questo modo :
"La somma della superficie dei 2 quadrati costruiti sui cateti, corrisponde alla somma della superficie del quadrato costruito sul lato dell'ipotenusa"

Ora che avete le formule di questo tipo di traingolo e conoscete il teorema di Pitagora, potete provare a risolvere questo semplice problema di geometria euclidea relativo ad un triangolo rettangolo. Dovrete naturalmente utilizzare le formule anche del teorema di Pitagora.
PROBLEMA SUL TRIANGOLO RETTANGOLO
"Un triangolo rettangolo presenta il lato obliquo l pari alla lunghezza di 30 cm (ipotenusa). La base del triangolo invece misura 24 cm (cateto). Calcolate la lunghezza dell'altezza h, pari all'altro cateto. Una volta trovata l'altezza h calcolate perimetro P e area A del triangolo rettangolo in questione"
Risultati :
h=18 cm
P=72 cm
A=216 cm quadrati
Questo problema è adatto a ragazzi di scuola media che abbiano studiato il teorema su esposto. Se desiderate approfondire le vostre conoscenze sulle figure geometriche allora provate a leggere questi altri miei articoli dove troverete problemi che potreste tentare di risolvere :








0 commenti:
Posta un commento